Antennenlaengen

Liebe Funkfreunde, wieder speziell an die "Newcomer" gerichtet und zum allgemeinen Verständnis.... Nach dem Projekt "Verlauf der HF-Spannungen auf einem Draht", welches sehr gut angenommen worden ist, kam öfters die Frage auf:"Wie lang muss denn nun ein Paralleldraht bzw. ein symetrisches Kabel sein, um eine Drahtantenne - Als Monoantenne oder als Dipole betrieben - anzuschliessen"? Die Antenne wurde nach dem Antennenlängenchart ausgewählt.

In der Fachliteratur findet man die Aussagen, dass eine Lambda/4 Parallelzuleitung und ungerade mehrfache Länge davon (3Lamda/4, 5Lambda/4 etc.), am Trx niederohmig und nach Lambda/4 sehr hochohmig ist oder umgekehrt (hochohmig auf niederohmig). So kann man einen niederohmigen TRX Ausgang an eine hochohmige Antenne oder einen hochohmigen Ausgang an eine niederohmige Antenne anschliessen. Man nennt diese Anpassung auch Tranformation. Ist die Parallelzuleitung Lambda/2 lang und mehrfaches davon, dann ist die Transformation 1:1, das heisst niederohmiger TRX auf niederohmige Antenne bzw. hochohmiger TRX auf hochohmige Antenne, was wohl kaum vorkommt.....

Aus diesem Grund habe ich mir Gedanken darüber gemacht auf einfachste Art und Weise die Anpasslänge der Parallelleitung darzustellen. Der Grundgedanke ist die eben beschriebene Erkenntnis Lambda/4 = niederohmig auf hochohmig und Lambda/2 = 1:1 Transformation. Die Wellenlänge Lambda ist bekanntlich 300/F(Mhz). Als Verkürzungsfaktor habe ich VF=0.91 angenommen. 300 ist die Umrechnung der Lichtgeschwindigkeit 300000 Km/s in m/s und Hz in Mhz.

Wenn nun Lambda als Gradzahl oder Radiant (2 Pi) aufgezeigt wird, dann ist am Anfang von Lambda=0° und am Ende 360 Grad. 360 Grad entsprechen auch 2 Pi. Der sin(0 Grad)=0, der sin(90 Grad)=1, sin(180 Grad)=0, sin(270 Grad)= -1 und sin(360 Grad)=0. Betrachtet man nun vorwärts den Sinnusverlauf der Spannung, also vom Anfang der Zuleitung aus für die einzelnen Amateurfunkfrequenzen in Abhängigkeit von der Zuleitungslänge L nach der Formel...:

f(LDraht)=Sin( 2 mal pi geteilt durch Lambda mal Länge der Parallelzuleitung) ---> f(L)=sin(2*pi/300/f(MHz)*LDraht(m))

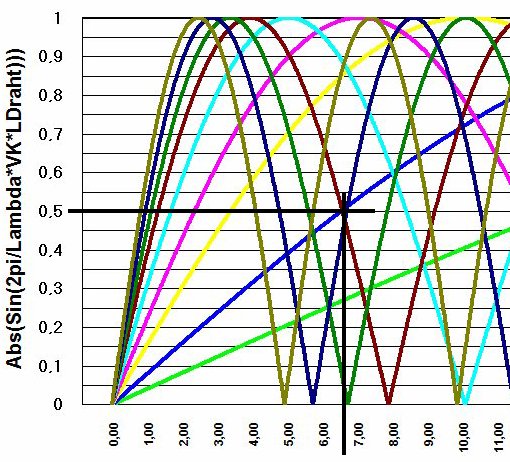
......und bildet jeweils den Absolutwert vom Ergebnis, um keine negativen Werte zu erhalten, dann bekommt man die Schaubilder, die nachfolgend abgebildet sind.

Bei der Drahtlänge wo sich Schnittlinien der Kurven ergeben, sind die physikalischen Verhältnisse für Z (abgesehen von den Reaktanzen) für den Einspeisepunkt gleich.

Die Daten für die Grafiken wurden mit einem Tabellenkalkulationsprogramm ermittelt.

Gerade für einen Neuling im Amateurfunk eine bildhafte Vorstellung, wie die Parallelzuleitung mit ihrer Transformation einen hoch oder niederohmigen Antennendraht oder Dipol anpasst. Wenn für den Wert "1" eine Grösse im KOhm - Bereich und bei 0 etwa 30 Ohm angenommen wird, kann man auch die Größe der Transformation abschätzen.

Die Werte 0 - 1 = 30 Ohm - 3 Kohm sind nicht linear. Aber bis etwa 0,5 = 500 Ohm und von 0,5 bis 1= 500 bis 3 Kohm abzuschätzen.

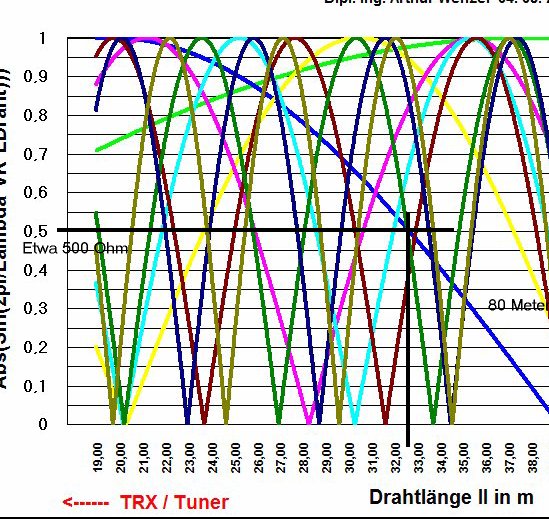
Angenommen sei eine Transformation für eine Eindrahtantenne, die im Einspeisepunkt ein Z von etwa 500 Ohm hat. Der Dipole hat dementsprechend eine Impedanz von etwa 1 KOhm. Die Anpassung soll für 80 Meterband sein. Nun sucht euch die Schnittpunkte bei 0,5 mit der blauen 80 Meterlinie. Da die Parallelleitung kleiner als Lamda/4 ist, ist diese induktiv. Gut zur Anpassung kapazitver - also zu kurzer Antennen!

Wir sehen aus dem Chart, dass am Ende der Zuleitung die Impedanz von ~500 Ohm bei etwa 6,5 Meter Paralleldraht und bei 32,5 Metern besteht und somit eine Antenne mit einer Eingangsimpedanz von 500 Ohm optimal anpasst. Dabei ist zu beachten, dass die Kabelimpedanz bei etwa 1000 Ohm liegt. Also etwa 200 mm Abstand der Leitungen und 1,5 mm Leitungsstärke. Bei Leitungsimpedanzen weniger 1000 Ohm geht auch die Reaktanz nach unten. Ist die Leitungsimpedanz 600 Ohm, dann sind es etwa 320Ohm Reaktanz am Ende der Leitung bei 6,5 m Länge und bei einer Leitung von 300 Ohm sind das dann nur noch 162 Ohm.... ALSO ACHTUNG immer kurz prüfen mit der nachfolgenden Formel!

Für die allgemeine Betrachtung der Reaktanz einer am Ende kurzgeschlossenen Hühnerleiter gilt:

Zr = Zo * tan(180 * l/Lambda) für Gradrechnung oder Zr = Zo * tan(pi * l/Lambda) für Radiantenrechnung

Zr ist die Reaktanz der Last, Zo die Eigenimpedanz der Leitung, l die Länge der Leitung und Lambda die Wellenlänge (300/Frequenz in Mhz) ist.

Für die allgemeine Betrachtung der Impedanz einer am Ende offenen Hühnerleiter gilt:

Zr = Zo * cot(180 * l/Lambda) für Gradrechnung oder Zr = Zo * cot(pi * l/Lambda) für Radiantenrechnung

Zr ist die Reaktanz der Last, Zo die Eigenimpedanz der Leitung, l die Länge der Leitung und Lambda die Wellenlänge (300/Frequenz in Mhz) ist. Bei Resonanzlänge bestehen Sonderfälle.

Gleichzeitig sehen wir, dass sich auch die braune Linie (17 Meterband) und die dunkelblaue Linie (12 Meterband) bei 6,5 Metern Paralleldrahtlänge und einen Wert von 0,5 schneiden sowie die dunkelgrüne (15 Meterband) bei 32,5m und einige andere, die in der Nähe sind. Also lassen sich mit diesen Zuleitungslängen auch mehrere Frequenzen anpassen, die 500 Ohm Anpassungstransformation benötigen. Dabei ist aber immer die Reaktanz zu prüfen ob sie induktiv oder kapazitiv ist.

Bei Lambda/4 und ungradiges Mehrfaches davon gilt: Zo² = Za * Ze ====> Parallelresonanzkreis

wobei Zo die Leitungsimpedanz, Za der Ausgang (oder auch Zr Reaktanzanpassung) und Ze die Eingangsimpedanz der Leitung ist.

Bei Lambda/2 und gradzahliges mehrfaches davon gilt: Ze = Za ====> Serienresonanzkreis

Bei Lambda/4 und ungradiges Mehrfaches davon gilt: Zo² = Za * Ze ====> Serienresonanzkreis

wobei Zo die Leitungsimpedanz, Za der Ausgang (oder auch Zr Reaktanzanpassung) und Ze die Eingangsimpedanz der Leitung ist.

Bei Lambda/2 und gradzahliges mehrfaches davon gilt: Ze = Za ====> Parallelresonanzkreis

Beim Betrachten der neuen Kurven immer daran denken: Nach links geht's zum TRX und nach rechts zum Einspeisepunkt an der Antenne genau eine andere Richtung als bei der "HF auf einem Draht" Kurven.